Better sprint planning with Bayes
Imagine you are working in a software development team doing Scrum with 2-week sprints. If you are part of a larger organisation, it is likely there are delivery goals that go beyond the next sprint, let’s call them milestones. Inevitably, someone from above is going to ask you:
“Are you on track? Are you going to make the next milestone?”
This is what happened to me recently, and I struggled to come up with an answer. Looking around, I realised that many people are answering this question mainly based on their part experiences and on their personality. Which means that if you are the one asking you need to take into account who in answering to properly interpret the answer.
As an example, a person saying “We are going to make it” means something different if the person is usually an optimist then if they are a pessimist. Could it be that the person answering your question now was previously involved in a project that despite being very late was miraculously on time in the end? How likely is it that this previous incident, which is unlikely to happen again, is affecting their current estimate. Remember, we all have biases and different biases from one another.
Additionally, unless you can see the future, there is no way to possible know what is going to happen. The current performance of the team, and your previous experiences can be a good indicator. But are you comfortable on giving a black and white “Yes/No” answer based only on those indicators? Somehow it does not feel right to me, because even if the things we know are pointing towards a clear “Yes” or “No”, the things we know we don’t know, and the things we don’t know we don’t know can skew this answer towards a “Possible Yes” or a “Maybe No”. So, I realised that there is a continuum of valid answers containing “Yes”, “No” and everything in between, and somehow I have to communicate where we are in this continuum.
I started looking on whether there is a more scientific approach in answering that question. An approach that would less influenced by human biases, and would allow me to also communicate the uncertainty inherent to my answer.
It is all about confidence!
So, I started reading my first book on statistics [1]. The cool things is that mathematicians have developed tools to deal with uncertainty. Either because you cannot predict the future, or because you don’t have access to 100% of the information.
Let’s understand a bit better the mathematical tools, and then we will circle back to our original question.
Imagine that someone gives you a coin and ask you if this coin is fair or crooked. In a fair coin the probability of getting heads is equal to the probability of getting tails, 50%. If the coin favors one side, or the other more than 50% of the time than it is crooked.
Not being an expert in coin making and without access to an X-Ray machine to scan the coin, you start tossing the coin to check if it behaves as expected.
Let’s say you toss a coin 10 times and you get 3 heads and 7 tails. Is this convincing evidence that the coin is crooked?
What is you toss it 100 times and you get 45 heads and 55 tails. Are you now convinced that the coin is fair?
This example shows a situation, that is so common in real life. You have to work with incomplete information, in the example you don’t know if the coin was manufactured to be fair or crooked but based on the information you gathered by tossing the coin you can induce whether the coin if fair or not. Importantly, we can never be completely sure for our answer, still our observations will make the one outcome more likely than the other.
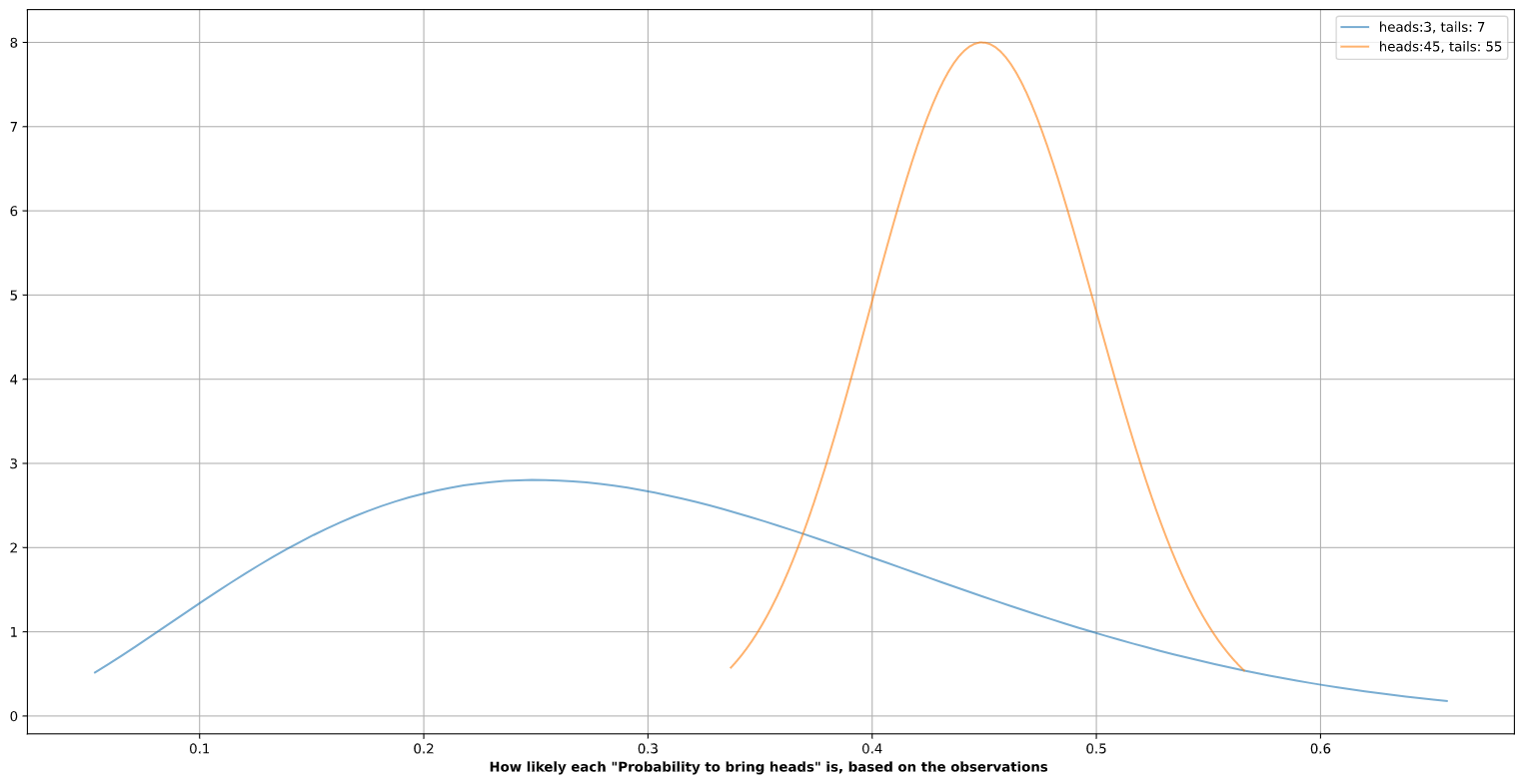
Back in the coin example, after 10 coin tosses, the most likely probability of bringing heads is ~0.25, but you can also that other probabilities like 0.2, 0.3 and even probabilities further away from 0.25 like 0.1 or 0.5 are still likely. To put it in another way, from what we know so far, it seems that the answer is 0.25 but other answers even very different 0.25 are possible.
After 100 coin tosses, most likely the probability of bringing Heads is ~0.45, but this distribution is much narrower. Which means we are very confident that the value 0.45 is correct or very close to the correct answer.
Sprint velocity
For those teams that are measuring their Sprint Velocity, you can use your historical data to generate a probability distribution showing the probability of completing N number of stories in a Sprint. Let’s call it the delivery probability distribution.
You can now transform the question on whether you will achieve the milestone in 3 months to the question, how likely is it that in the next 6 sprints we will complete all N stories that you need to achieve the milestone.
Monte Carlo
In the “Avengers: Infinity War”, when the Avengers are in a dire situation, Doctor Strange looks into all possible futures. Finally, saying that only in 1 in 14 million outcomes they actually win.
You can use the same strategy in your project! In order to communicate not only the most plausible outcome but also your confidence level that this outcome will be achieved.
Using the Monte Carlo methodology, you can generate sequences on random numbers based on the delivery probability distribution, as a simulation of how your future sprints may look like. In this simulation, do you manage to complete enough stories to achieve the milestone?
Now repeat the previous exercise hundreds or thousands of times. In how many of those simulations do you achieve your goal?
Now, you can communicate this number with your manager. This number is not only less prone to personal biases. It also allows meaningful discussions, like are we comfortable we the current confidence level? Do we have to act now?
Also keeping track this number over time make reporting easier. So long as the confidence level, remain high and stable, you can reduce the time spend on reporting and rather focus on actual delivery. Now, if the number starts to drop, it can act as early warning sign, drawing your attention to the problem before it becomes an issue.
Conclusion
In this blog post, I discuss a method for more objective sprint planning and forecasting.
The main idea is to compute the odds of achieving your goal using your historical velocity, statistics and Monte Carlo simulations. This process will give you the odds of achieving your goal. Those odds are what you use for reporting.
The odds are a method track and communicate uncertainty.